Lernkontrolle
Ausgangslage/Problemstellung:
Ein durchschnittlich trainierter
Jogger/Joggerin braucht 2,5h nach dem Mittagessen für 1km Strecke 5 Minuten. Diese
Leistung gilt als Standardwert. Die Populationsstandardabweichung beträgt 0,5
Minuten.
Nach einer letzten Seminarveranstaltung vor den
Sommerferien verabreden sich die 36 Studierenden zu einem Mittagessen. Als "krönenden
Abschluss" beschliessen sie, gleich nach dem Mittagessen eine Joggingrunde von einem
Kilometer zu bewältigen. Während des Umkleidens findet Leo, er möchte - angesichts des
übermässig gefüllten Magens - die ganze Unternehmung nur mental durchstehen. Er verspricht
den anderen, durch seine Joggingabstinenz einen Beitrag zur Grundlagenforschung zu
leisten. Er wertet die Joggingleistung der anderen statistisch aus. Die Joggenden brauchen
für einen Kilometer durchschnittlich 7 Minuten. Die Standardabweichung beträgt 0,75
Minuten.
Auftrag
Prüfen Sie die Aussage des Titels (plenus venter non joggt libenter) mit statistischen Mitteln.
Lösung des Übungsbeispiels
| Leitfaden zum Mittelwertvergleich | Lösung von "plenus venter non joggt libenter" |
|---|---|
| 1. Formulieren Sie eine inhaltliche Frage zur Problemstellung. | Brauchen die Studierenden nach dem Mittagessen durchschnittlich tatsächlich länger, um eine Joggingstrecke von einem Kilometer zu bewältigen, oder kann der Unterschied von zwei Minuten zufällig entstanden sein? |
| 2. Formulieren Sie eine statistisch bearbeitbare Frage. | Stammen die Studierenden, die gerade das Mittagessen verspiesen haben, aus einer Population, die hinsichtlich der mittleren Joggingzeit identisch ist mit der Population der Joggerinnen und Jogger, die das Mittagessen bereits verdaut haben? |
| 3. Bestimmen Sie die Prüfgrösse und formulieren Sie die Arbeitshypothese H0 und die Alternativhypothese H1. | Prüfgrösse: 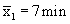 Arbeitshypothese H0: 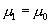 Alternativhypothese H1: 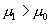 Aufgrund der gerichteten Fragestellung formulieren wir eine gerichtete, unspezifische Alternativhypothese. |
| 4. Bestimmen Sie die Prüfverteilung. | Unter der Annahme, dass H0 gültig
ist, sind Stichprobenmittelwerte von Zufallsstichproben der Grösse n > 30 mit den
Parametern 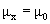 und und
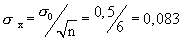 normalverteilt.
normalverteilt.
|
| 5. Transformieren Sie die Prüfgrösse in die Standardnormalverteilung (z-Verteilung). | Leo transformiert den Stichprobenmittelwert in die standardisierte
Normalverteilung (z-Verteilung). 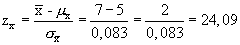 |
| 6. Entscheiden Sie aufgrund der Überschreitungswahrscheinlichkeit, ob Sie H0 ablehnen oder nicht ablehnen können. | Wir prüfen eine gerichtete Fragestellung. Der Ausprägungsgrad von 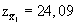 ist in unserer einfachen
Tabelle nicht zu finden, die Überschreitungswahrscheinlichkeit p ist aber sicher
kleiner als 0,1%. Die Arbeitshypothese H0 wird mit einer Irrtumswahrscheinlichkeit p
< 0,1% zu Gunsten von H1 abgelehnt ist in unserer einfachen
Tabelle nicht zu finden, die Überschreitungswahrscheinlichkeit p ist aber sicher
kleiner als 0,1%. Die Arbeitshypothese H0 wird mit einer Irrtumswahrscheinlichkeit p
< 0,1% zu Gunsten von H1 abgelehnt
|
| 7. Interpretieren Sie das Prüfungsergebnis. | Der Titel spricht mit einer sehr kleinen Unsicherheit die Wahrheit: Ein voller Bauch joggt nicht gern. |