Damit Sie die Wahrscheinlichkeit bestimmen können, mit welcher der Stichprobenmittelwert 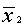im Rahmen der Prüfverteilung zufällig erreicht oder überschritten wird, transformieren Sie 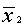in die t-Verteilung: .

Die Transformation entspricht der besprochenen z-Transformation. Da die Prüfgrösse t-verteilt ist (Freiheitsgrad df = n-1), benutzen wir aber zur Bestimmung der Überschreitungswahrscheinlichkeit p die t-Tabelle für die t-Verteilung mit dem Freiheitsgrad df. Da wir eine gerichtete Fragestellung untersuchen und der Arbeitshypothese H₀ eine gerichtete Alternativhypothese H₁ gegenüberstellen, suchen wir die einseitige Überschreitungswahrscheinlichkeit für den t-transformierten Ausprägungsgrad der Prüfgrösse.

Jetzt konsultieren Sie die t-Tabelle. Beachten Sie dabei den Aufbau der t-Tabelle. (So wird z.B. die Tabelle D (Hirsig, 2001) für einseitige Hypothesenprüfung von unten gelesen.)

Zur Veranschaulichung nehmen wir an, dass df = 24 und 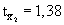sei. Die folgende Darstellung zeigt die Einordnung des Ausprägungsgrades der Prüfgrösse in die Liste der Grenzwerte der t-Verteilung mit df = 24.



Die Überschreitungswahrscheinlichkeit vo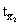n ist grösser als 5%. Sie können H₀ nicht ablehnen. Das bedeutet, dass Sie nicht ausschliessen können, dass Ihre Stichprobe 2 aus einer Population 2 stammt, die hinsichtlich des Mittelwertes mit der bekannten Population 0 identisch ist. Der positive Unterschied zwischen dem Stichproben- und dem Populationsmittelwert kann zufällig entstanden sein. Eine Irrtumswahrscheinlichkeit kann nicht angegeben werden.