In diesem Schritt transformieren Sie den Mittelwert in die standardisierte Normalverteilung.

Die entscheidenden Daten sind:

• : Populationsmittelwert der Population 0
• : Mittelwert der Verteilung der Stichprobenmittelwerte (Prüfverteilung).
• : Standardabweichung der Verteilung der Stichprobenmittelwerte (Prüfverteilung).
• : Mittelwert der Stichprobe 1.
• : z-transformierter Stichprobenmittelwert.

Die Transformation nehmen Sie anhand dieser Formel vor:



Da Sie jetzt kennen, können Sie anhand der z-Tabelle die Überschreitungswahrscheinlichkeit bestimmen, mit der zufällig erreicht oder überschritten wird.

Soll die einseitige oder die zweiseitige Überschreitungswahrscheinlichkeit bestimmt werden?

Zur Beantwortung dieser Frage müssen Sie sich unsere Fragestellung nochmals vergegenwärtigen: Stammt die Stichprobe 1 aus einer Population 1, die hinsichtlich des Mittelwertes mit der bekannten Population 0 identisch ist?

Diese Frage berücksichtigt das Vorzeichen eines allfälligen Unterschiedes nicht, somit handelt es sich um eine zweiseitige oder ungerichtete Fragestellung.

Vorschlag zur Vertiefung

• Einzelarbeit: Erstellen Sie eine Skizze von der Standardnormalverteilung, tragen Sie für die zweiseitige Fragestellung ein und markieren Sie die Wahrscheinlichkeit, mit der zufällig erreicht und über- bzw. unterschritten wird. Beschriften Sie die Skizze.
• Gruppenarbeit: Jedes Gruppenmitglied erstellt eine Skizze von der Standardnormalverteilung, trägt für die zweiseitige Fragestellung ein und markiert die Wahrscheinlichkeit, mit der erreicht und über- bzw. unterschritten wird. Beschriften Sie die Skizze und diskutieren Sie miteinander die Lösungen. Klären Sie abweichende Lösungsvorschläge.
• Die Antwort auf den Vertiefungsvorschlag erhalten Sie auf der nächsten Theorieseite.

Die Graphik illustriert die zweiseitige Überschreitungswahrscheinlichkeit für unsere ungerichtete Fragestellung. (ungerichtete Alternativhypothese H₁)

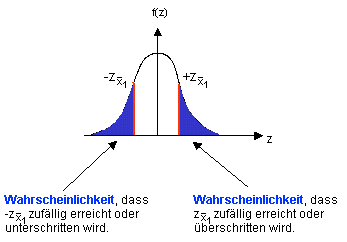
Jetzt verfügen Sie über alle notwendigen Informationen und können im nächsten Schritt die zweiseitige Überschreitungswahrscheinlichkeit der entsprechenden z-Tabelle entnehmen.

Das folgende Beispiel zeigt, wie die zweiseitige Überschreitungswahrscheinlichkeit bestimmt wird. Wir nehmen an, dass sei.