| 1. Formulieren Sie eine inhaltliche Frage zur Problemstellung. |
Bleibt identisch. |
| 2. Formulieren Sie die Frage so, dass sie statistisch bearbeitbar
ist.
|
Bleibt identisch. |
| 3. Bestimmen Sie die Prüfgrösse und formulieren Sie die Arbeitshypothese
H0 und die Alternativhypothese H1.
|
Bleibt identisch. |
4. Bestimmen Sie die Prüfverteilung: Unter der Annahme, dass H0 gültig ist, sind die Stichprobenmittelwerte mit den
Parametern 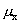 und und 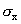 normalverteilt. normalverteilt.
|
Sie müssen voraussetzen, dass das Merkmal in der Population näherungsweise
normalverteilt ist (das zentrale Grenzwerttheorem gilt nicht). Unter der Annahme, dass
H0 gültig ist, sind die
Stichprobenmittelwerte mit df= (n-1) und den Verteilungsparametern 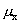 und und 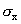 t-verteilt. t-verteilt.
|
| 5. Transformieren Sie die Prüfgrösse in die Standardnormalverteilung
(z-Verteilung).
|
Transformieren Sie die Prüfgrösse in die tabellierte
t-Verteilung.
|
| 6. Entscheiden Sie anhand der Überschreitungswahrscheinlichkeit, ob Sie
H0 ablehnen oder nicht ablehnen können. Je
nachdem, ob sie gerichtet oder ungerichtet prüfen, wählen Sie die Tabelle für
einseitige oder zweiseitige Überschreitungswahrscheinlichkeiten. Konsultieren Sie die
z-Tabelle.
|
Bleibt identisch, ausser: Konsultieren Sie die t-Tabelle unter
Berücksichtigung des Freiheitsgrades df = (n-1).
|
| 7. Interpretieren Sie das Prüfungsergebnis. |
Bleibt identisch. |
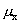 und
und 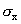 normalverteilt.
normalverteilt.
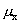 und
und 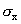 t-verteilt.
t-verteilt.