Andere Bezeichnungen

Zentralwert, zentraler Wert

Charakterisierung

Nachdem die Ausprägungsgrade in eine Rangreihe gebracht wurden, kann der Median M_d bestimmt werden: Liegen über einem Wert genau so viele Ausprägungen wie unter diesem Wert, so wird dieser Wert als Median M_d bezeichnet.

Voraussetzungen

Da zur Bestimmung des Medians M_d die Ausprägungswerte in eine Rangordnung gebracht werden müssen, kann der Median M_d nur bestimmt werden, wenn das Merkmal mindestens ordinal skaliert ist.

Eignung

Im Gegensatz zum arithmetischen Mittel wirken sich einzelne extrem hohe oder extrem tiefe Ausprägungsgrade (Ausreisser oder Extremwerte) nicht auf den Median M_d aus. Es spielt somit keine Rolle, ob einzelne Werte weit oberhalb oder unterhalb des Medians M_d liegen. Dies bedeutet, dass der Median M_d or allem dann besonders nützlich ist, wenn stark asymmetrische (schiefe) Verteilungen oder Verteilungen mit einigen sehr extremen Werten beschrieben werden sollen.

Hinweise und zusätzliche Erklärungen

Medianbestimmung bei ungerader Zahl von Beobachtungen und nur einmal vorkommenden Ausprägungsgraden bei intervall-skalierten Merkmalen

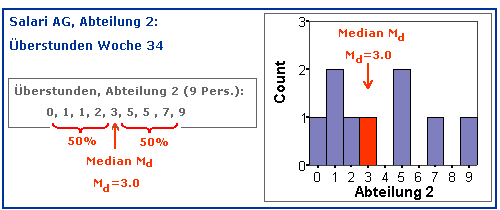
Die Berechnung des Medians M_d ist einfach, wenn ein Datensatz eine ungerade Anzahl von Beobachtungen aufweist.

Medianbestimmung bei gerader Zahl von Beobachtungen und nur einmal vorkommenden Ausprägungsgraden bei intervall-skalierten Merkmalen

Bei ungerader Zahl von Beobachtungen berechnet sich der Median M_d als arithmetischer Mittelwert der beiden zentralen Werte der geordneten Datenreihe.

Medianbestimmung bei Häufigkeitsverteilungen bei intervall-skalierten Merkmalen

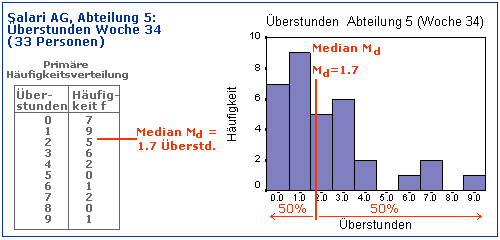
Bei Häufigkeitsverteilungen kann der Median M_d nicht so einfach bestimmt werden. Mit einer linearen Interpolation kann der Median M_d jedoch auch in diesem Fall entweder manuell oder mit der Statistiksoftware SPSS näherungsweise bestimmt werden. Wie aus der Abbildung ersichtlich ist, entspricht der Median M_d in diesem Fall keinem tatsächlich beobachteten Ausprägungsgrad.

Medianbestimmung bei ordinal skalierten Merkmalen

Bei ordinal skalierten Daten mit einer graden Anzahl von Beobachtungen und nur einmal vorkommenden Ausprägungsgraden ist es nicht möglich, die Werte der beiden mittleren Fälle zu halbieren wie bei intervall-skalierten Daten. Man beschränkt sich deshalb darauf anzugeben, zwischen welche zwei Beobachtungen der Median M_d zu liegen kommt.
Bei Häufigkeitsverteilungen kann bei ordinal skalierten Merkmalen eine lineare Interpolation nicht durchgeführt werden. Die Suche nach dem Median M_d beschränkt sich deshalb auf die Identifizierung der Kategorie, in die der Median M_d fällt.